本文最后更新于 2024年4月30日 晚上
微分几何入门与广义相对论 Chapter2
微分几何入门与广义相对论 Chapter2
第二章 流形和张量场
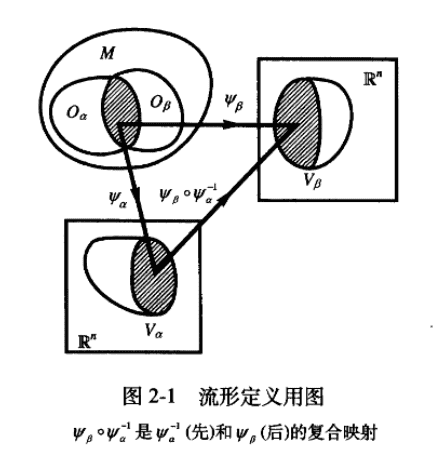
定义1 拓扑空间称为维微分流形(-dimensional differentiable manifold),简称维流形,若有开覆盖,即,满足:(a),(是用通常拓扑衡量的开子集);(b)若,则复合映射(见图)是(光滑)的.
/notes/
局部地看,一个维微分流形与一个没有差别(上面定义中的同胚可以看出这一点).
上述定义的是光滑流形. 把上述定义中的换成就是流形的定义.
这个复合映射指的是先进行再进行.
是从到的映射. 这给出了个元函数,它们都是的(是的).
设,则,故点有个自然坐标. 很自然地把这个数称为点在映射下获得的坐标作为拓扑空间,其元素本来一般没有坐标,但作为流形, 中位于 内的元素(点)就可通过映射获得坐标. 若,则内的点既可通过又可通过获得坐标,这两组坐标一般不同. 我们说()构成一个(局域)坐标系(coordinate system), 其坐标域(coordinate patch)为构成另一坐标系,其坐标域为. 于是内的点至少有两组坐标,分别记作和. 由映射提供的、体现两组坐标之间关系的n个n 元函数
就称为一个坐标变换(coordinate transformation). 定义1条件(b)保证坐标变换中的函数关系 都是 的. 为方便起见也常称 为坐标系,虽然从中看不出坐标域的范围. 物理学家也常把记作.
定义2 坐标系在数学上又叫图(chart),满足定义1的全体集合叫图册(atlas). 条件(b)又叫相容性(compatibility)条件,因此说一个图侧重的任意两个图都是相容的.
例1 设. 选,恒等映射(即像与逆像重合的映射),则便是只含一个图的图册,故是2维流形,而且是能用一个坐标域覆盖的流形,称为平凡流形.
同理可知是维平凡流形.
例2 ,是里的一个圆周. 我们来证明它是一个manifold. 我们猜测(直观来看),认为它是一维的,将要映射到上去. 这里显然不能只用一个图来映射,因为与不同胚. 所以我们用四个图来覆盖,分别是左半圆周、右半圆周、上半圆周和下半圆周,均为的通常拓扑所产生的诱导拓扑中的开集,此时它可以被完全覆盖,每个图中的映射就是将圆周投影到对应方向的数轴上去. 证毕.
例3 ,也就是二维球面. 在这里提到,sphere是球面,而ball是实心的球体,注意作出区分. 是三维中的二维球面,可以用两个坐标表示上面的点. 显然,这个球面是manifold. 类似上面例2的证明,我们用6个图来覆盖整个球面,均为的诱导拓扑中的开子集,每个映射也是投影. 至此证毕.
对于一个拓扑空间,可以定义不同的拓扑;对微分流形的定义,也有不同图册的选择:和. 若,则它们有可能是相容的(compatible),这就是说在定义里的那个映射是的.
这时有两种情况:相容和不相容. 若不相容,则这两个图册将同一个底拓扑定义为两个不同的微分流形,它们的微分结构不相同. 注意,微分结构要在之后的学习中不断地领会,循序渐进,所以暂时不做更深讨论.
若相容,两个图册定义的微分流形是一样的. 我们可以造出一个更大的图册来包含它们,所以今后我们定义图册时,默认用最大的图册.
这体现出一个好处,最大图册中间的任意图之间都可以方便地做坐标变换. 图与图之间的变换就是坐标变换.
/notes/
坐标系都有坐标域,坐标变换一定是连续的(),不能说它们是奇异的,出现问题只是因为超出了其对应的坐标域.
定义3 称为类映射,如果,映射对应的个元函数是类的.
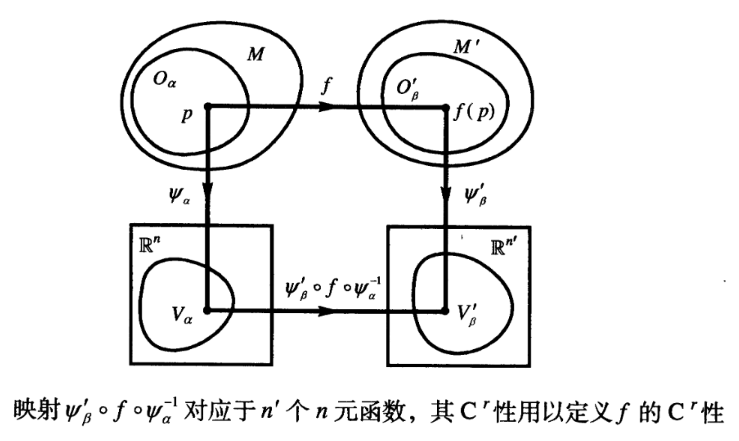
注意,和都是同胚映射. 所以的性能转化为的性.
/notes/
如果不是微分流形,就不能定义上述连续性,这是微分流形和普通拓扑空间之间的区别.
同时,由于同一图册中各图相容,上述定义与坐标系及的选择无关.
定义4 微分流形和称为互相微分同胚(diffeomorphic to each other),若,满足(a)是一一到上的;(b)及是的. 这样的称为从到的微分同胚映射,简称微分同胚(diffeomorphism).
/notes/
微分同胚是强于同胚的,是对流形之间的映射提出的最高要求.
微分同胚的两个流形维数必须相等.
定义5 称为上的函数(function on )或上的标量场(scalar field on ). 若为的,则称为上的光滑函数. 上全体光滑函数的集合记作,在不会混淆时简记为. 今后在提到函数而不加声明时都是指光滑函数.
/notes/
注意,这里的函数与微积分学里的函数并不相同. 它不是所谓的元函数,如果想让它成为多元函数,必须引入坐标系. 而引入不同的坐标系,多元函数本身的形式变了,函数值却是一样的. 这里的函数是不需要坐标系的,不能理解为元函数.
标量场是“父亲”,与不同的坐标系结合,生出不同的“儿子”(多元函数).
为了不造成混淆,我们还是一直用“标量场”这一名词. 同时,说标量场是“绝对的”,而其与坐标系结合产生的“多元函数”是“相对的”.
例4 中位于点的点电荷的电势是流形上的光滑函数.
注:从例3开始看梁老师的课,决定边听课边敲笔记.
2.2.1 切矢量
定义1 实数域上的一个矢量空间(vector space)是一个集合配以两个映射,即 [ 叫加法(addition)] 及 [ 叫数乘(scalar multiplication)] ,满足如下条件:
/notes/
由(g)可推出:.
今后把零元记为0.
在我们平常讨论的问题中,矢量指的是中的一个“箭头”. 但是以上的定义包含了平常我们讨论的矢量,是一个更广泛的概念. 在这里,我们将“箭头”所代表的概念从推广到任意微分流形.
在一个任意的微分流形中,“箭头”的意义不易推广,因为它有“方向”和“长度”,太具体则不易推广. 所以我们寻找矢量抽象的共性.
考虑上所有的映射,这个集合记为. 对于,有,存在,我们可以对求方向导数,并在所研究的点取值. 由于方向导数的操作有线性性并满足莱布尼兹律,所以本质的、便于推广的特性是:它是一个从到的、满足莱布尼兹律的线性映射. 推广到任意流形的任意点,定义:
定义2 映射称为点的一个矢量(vector),若,有
这里映射的方式还很多,所以点有无限多矢量. 作为例子,定义一些矢量:设坐标系,其坐标为,则上的光滑函数对应元函数,可给中任一点定义个矢量,记作,作用于任一的结果定义为如下实数
注:定理2-2-1在选读中,不写.
定理2-2-2 以代表中点所有矢量的集合,则是维矢量空间(是的维数),即.
证明
(A) 按以下定义加法、数乘和零元,不难验证满足定义,是矢量空间.
(B) 只需证明最大线性无关基矢的数量为,大于等于,且小于等于.
任选坐标系使得坐标域含,则上面定义了点的个矢量,. 欲证线性独立,设有个实数使(爱因斯坦惯例),则要证, .

